Lorenz - программа для изучения системы Лоренца
- Подробности
- Опубликовано: 10.07.2018 11:13
- Автор: Степанов Дмитрий Юрьевич
- Просмотров: 18160

Операционная система: Windows.
Лицензия: бесплатно.
Версия: 1.1.0.0.
Аннотация: демонстрируется программа для анализа системы Лоренца, позволяющая наблюдать такие состояния системы, как устойчивый аттрактор, два неустойчивых аттрактора, фокус, гомоклиническая петля с устойчивым и неустойчивыми фокусами, аттрактор Лоренца, предельный цикл и удвоенный предельный цикл.
Скачать: ZIP (архив программы).
Ключевые слова: аттрактор Лоренца, система Лоренца, исследование системы дифференциальных уравнений Лоренца, аттрактор Лоренца matlab, исследование системы Лоренца, аттрактор Лоренца c++, эффект бабочки, гомоклиническая петля, фазовый портрет Лоренца, фазовый портрет системы Лоренца, фазовое пространство Лоренца, решение системы лоренца, странный аттрактор Лоренца, бабочка Лоренца, гомоклиническая траектория, гомоклиническая структура, хаотическое решение, Эдвард Лоренц.
Система Лоренца представляет собой трехмерную систему нелинейных автономных дифференциальных уравнений. Динамическая система была исследована Эдвардом Лоренцем в 1963 году. Основной причиной, породившей такой интерес к системе уравнений Лоренца, является ее хаотическое поведение. Система уравнений записывается в виде
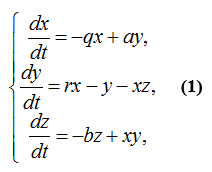
где q, r, b > 0. В результате интегрирования системы были выявлены закономерности, приведенные ниже.
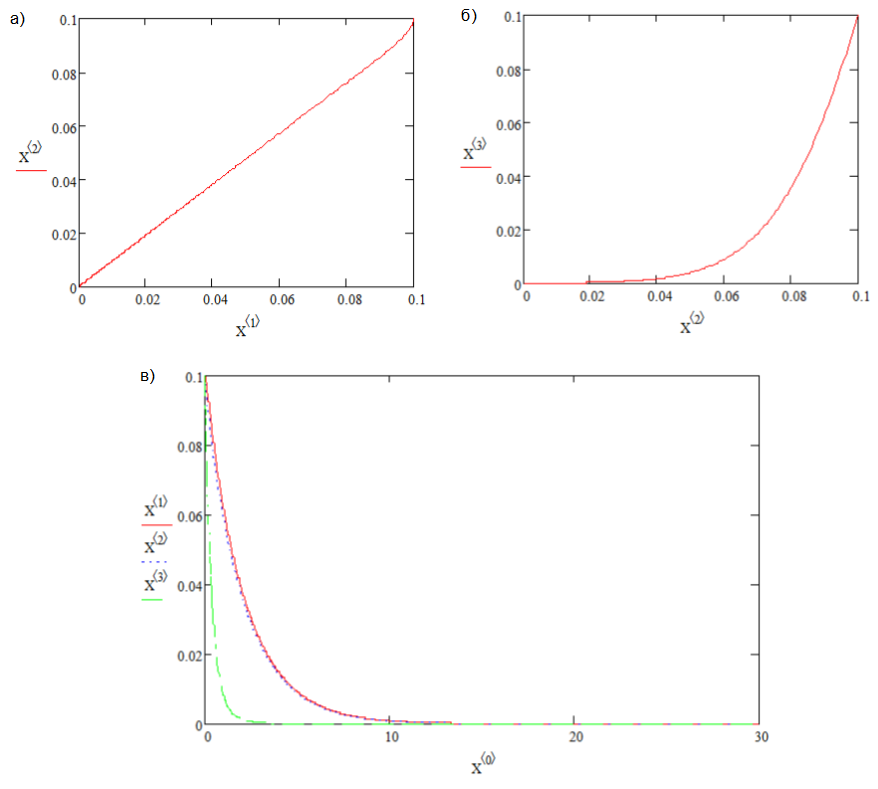
При r>0 и r<1 система имеем только одну критическую точку. Она является одновременно локальным и глобальным аттрактором. Любое начальное состояние приближается к началу координат при t стремящемся к бесконечности (рис.1).
Рис. 1. Устойчивый аттрактор, r>0 и r<1
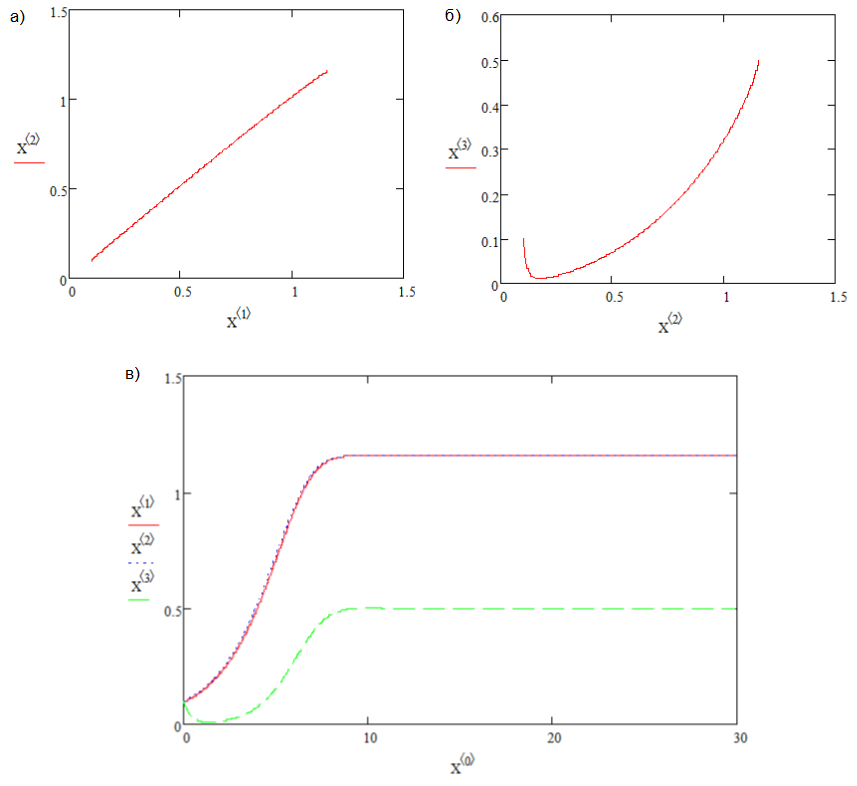
При r близкой к 1 возникает критическое замедление. Когда r превышает значение 1, происходит первая бифуркация. Начало координат теряет устойчивость и от него ответвляются два аттрактора (рис.2), оба глобально и локально устойчивы.
Рис. 2. Два устойчивых аттрактора, r>1
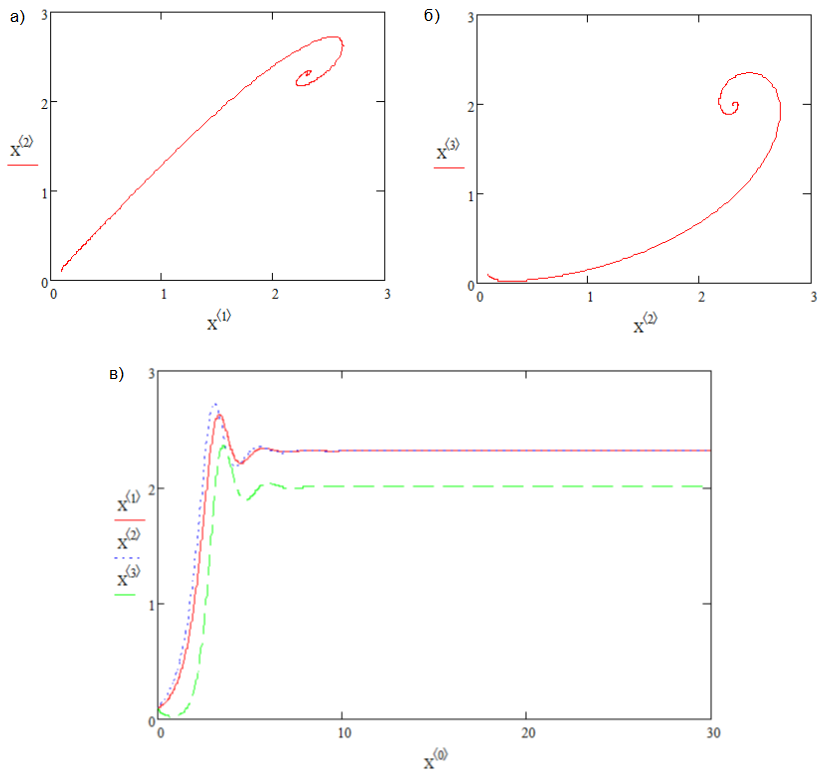
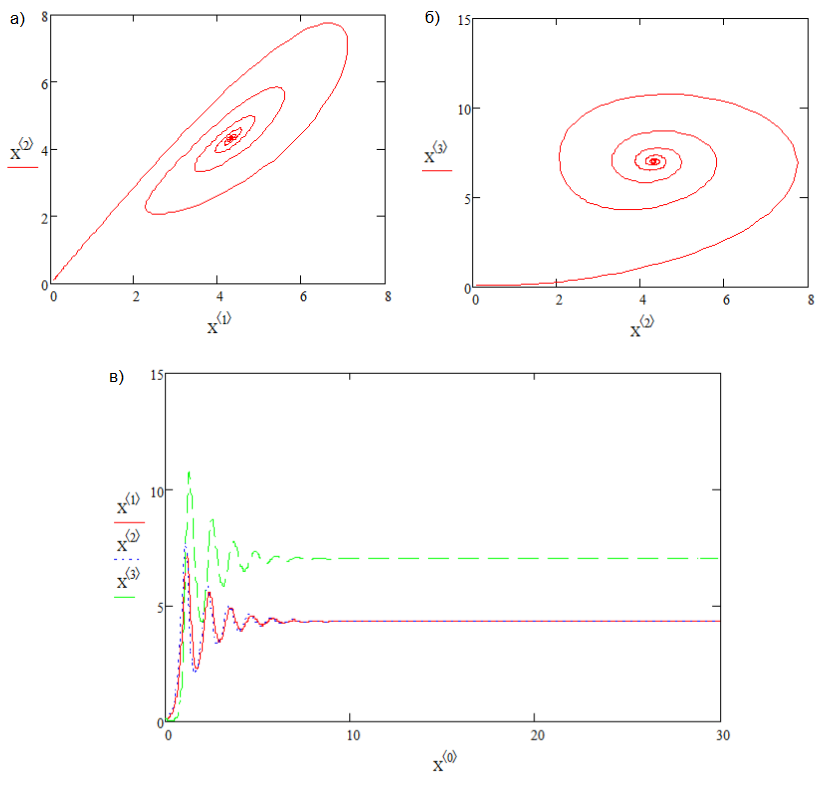
В случае r<1,345 точки равновесия представляются узлами (рис.3), а при r>1,345 – фокусами (рис.4).
Рис. 3. Два узла, r=1,3
Рис. 4. Два фокуса, r=10
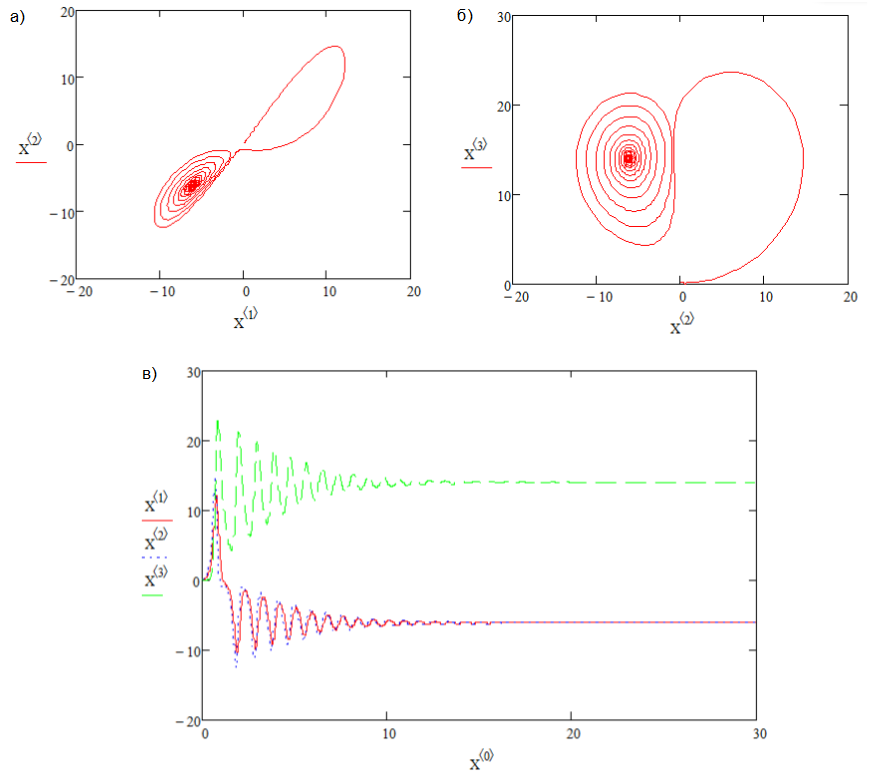
При увеличении r до величины 13,926 две неустойчивые траектории, исходящие из начала координат, возвращаются в начало координат при t стремящемся к бесконечности, при этом перестают быть глобальными аттракторами.
В случае r=13,927 точка может совершать колебательные движения из одной окрестности в другую и обратно. Такое поведение называют метастабильным хаосом или гомоклинической петлей (рис.5).
Рис. 5. Гомоклиническая петля, r=13,927
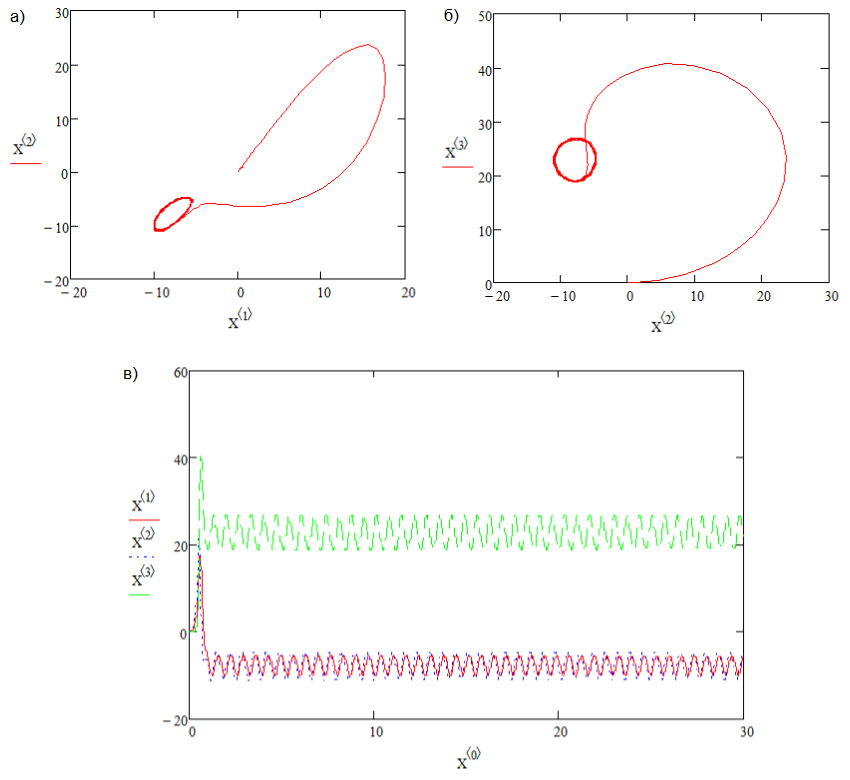
При r>13,927 в зависимости от направления траектория приходит в одну из двух устойчивых точек. Гомоклинические петли перерождаются в неустойчивые предельные циклы, также возникает семейство сложно устроенных траекторий, не являющееся аттрактором. Происходит бифуркация гомоклинических траекторий с образованием двух неустойчивых циклов (рис.6).
Рис. 6. Два неустойчивых цикла, r>13,927
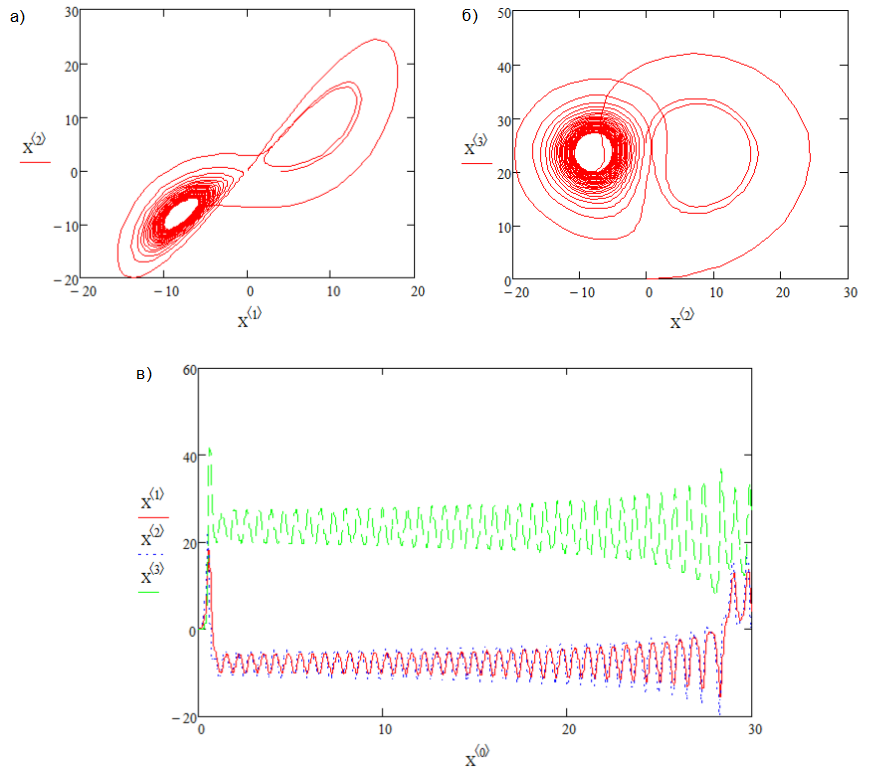
При значении r=24,06 траектории ведут не к устойчивым точкам, а асимптотически приближаются к неустойчивым предельным циклам — возникает собственно аттрактор Лоренца (рис.7).
Рис. 7. Аттрактор Лоренца, r=24,06
В случае r>24,06 происходит очередная бифуркация. Однако обе устойчивые точки сохраняются вплоть до значений r=24,74.
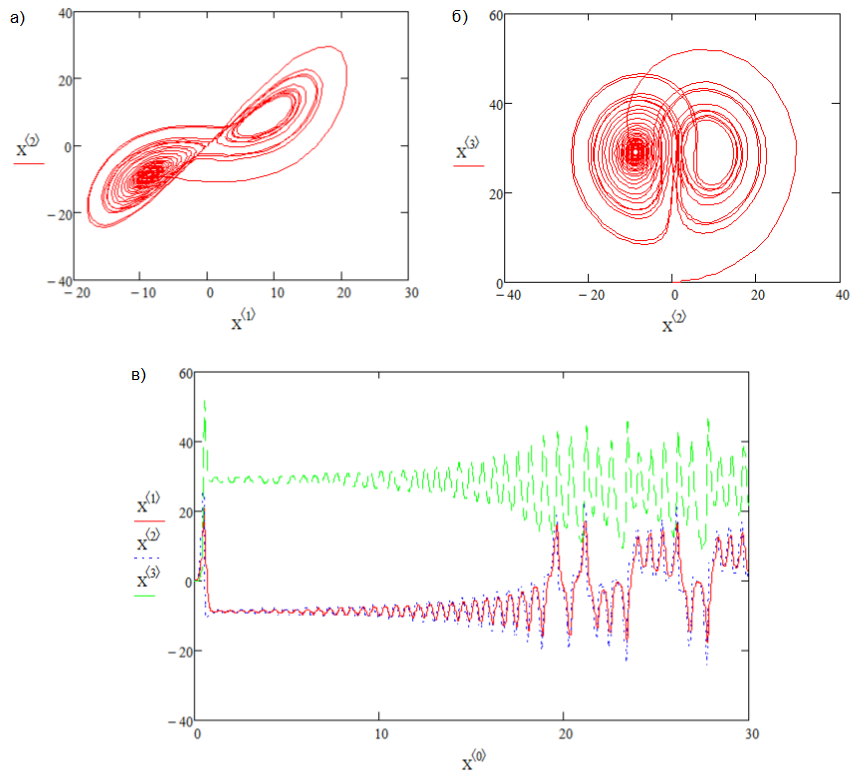
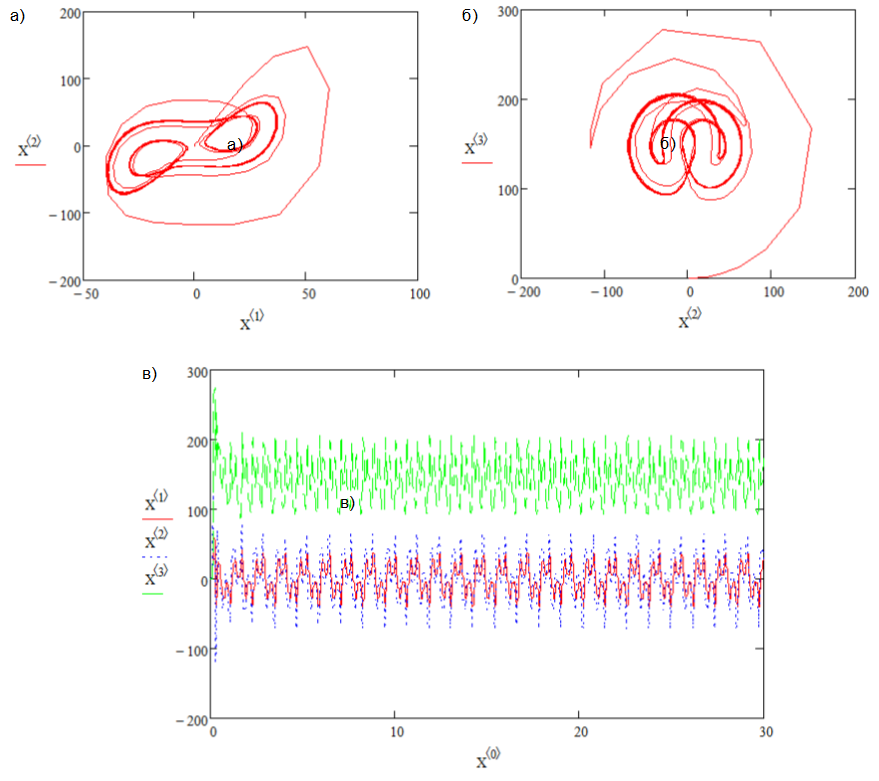
При r=24,74 возникает инверсия бифуркации Хопфа, когда r>24,74 остается «странный аттрактор» (рис.8).
Рис. 8. Странный аттрактор Лоренца, r>24,74
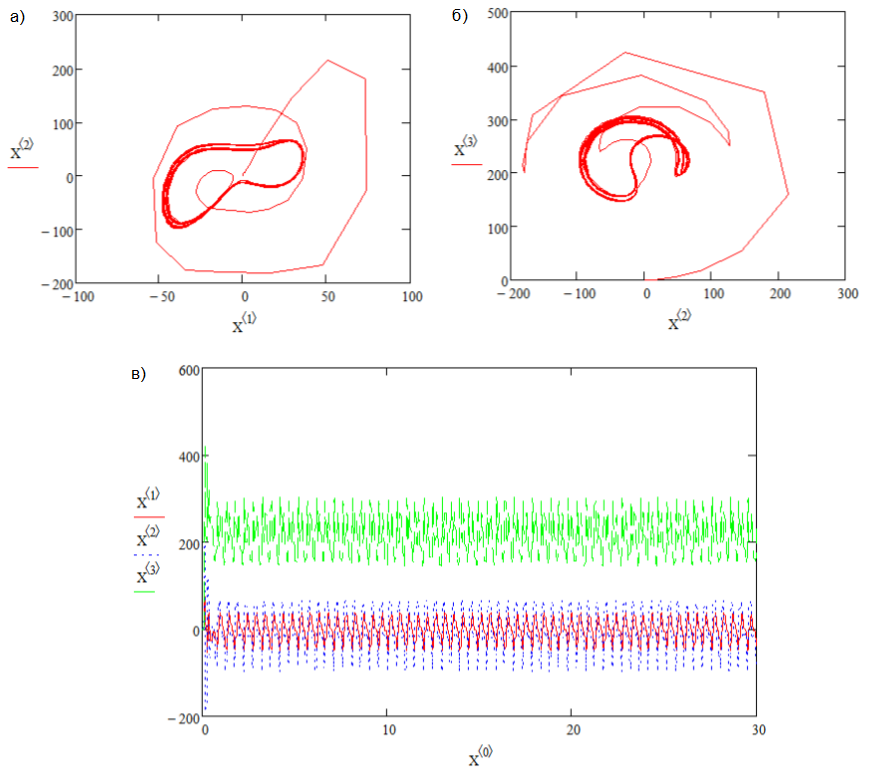
В случае увеличения r до 100 наблюдается автоколебательный режим (рис.9).
Рис. 9. Автоколебательный режим, r=100
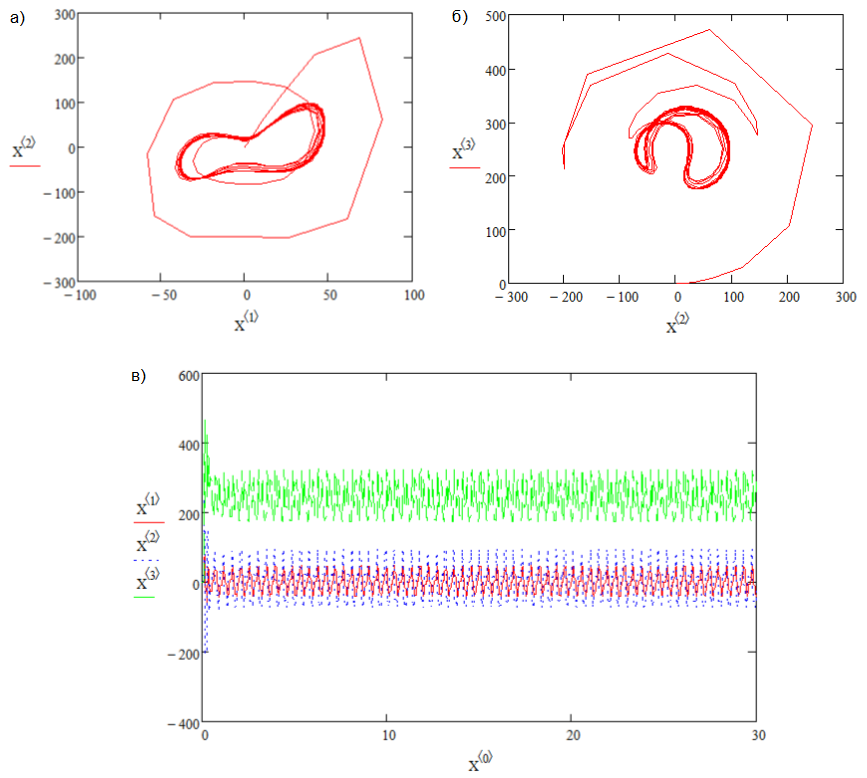
При увеличении r до значения 225 происходит каскад бифуркаций удвоения цикла (рис.10).
Рис. 10. Удвоение цикла, r=225
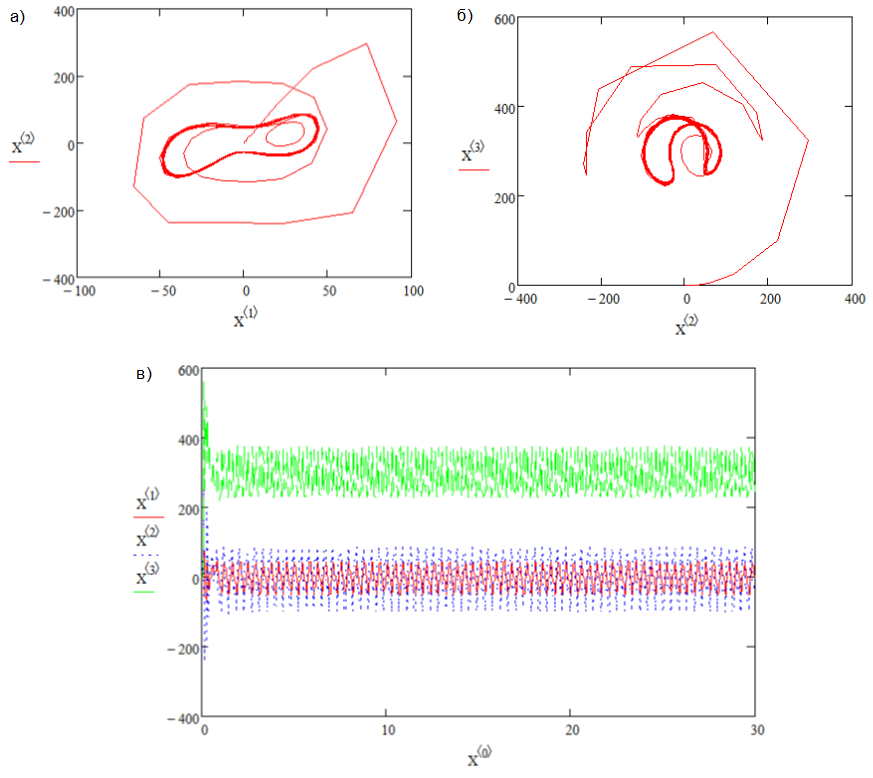
Далее при увеличении параметра r происходит бифуркация потери симметрии, и в системе существуют два несимметричных периодических решения. Пример поведения системы для r=300 дан на рис.11.
Рис. 11. Два несимметричных периодических решения, r=300
При больших значениях r в системе существует симметричный цикл (рис.12).
Рис. 12. Симметричный цикл, r=400
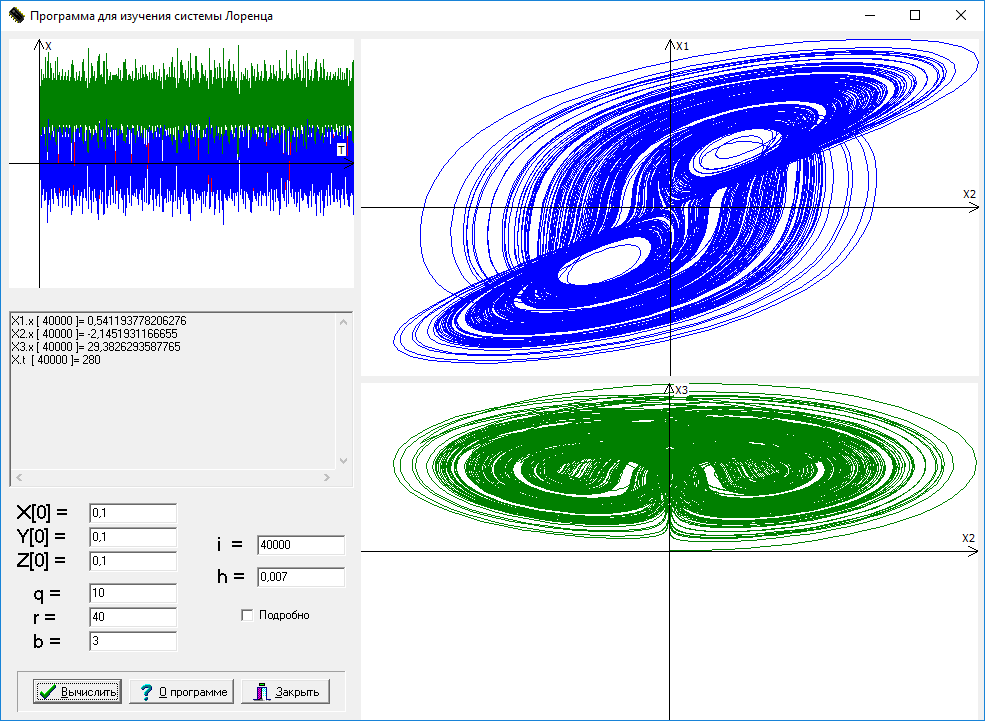
Программа «Lorenz - программа для изучения системы Лоренца», реализованная в среде разработки Turbo C++, позволяет смоделировать систему Лоренца. Построение фазовых портретов и графика зависимости решений от времени t ведется на основе метода Рунге-Кутта третьего порядка. Интерфейс программы приведен на рис.13.
Рис. 13. Интерфейс программы для изучения работы системы Лоренца
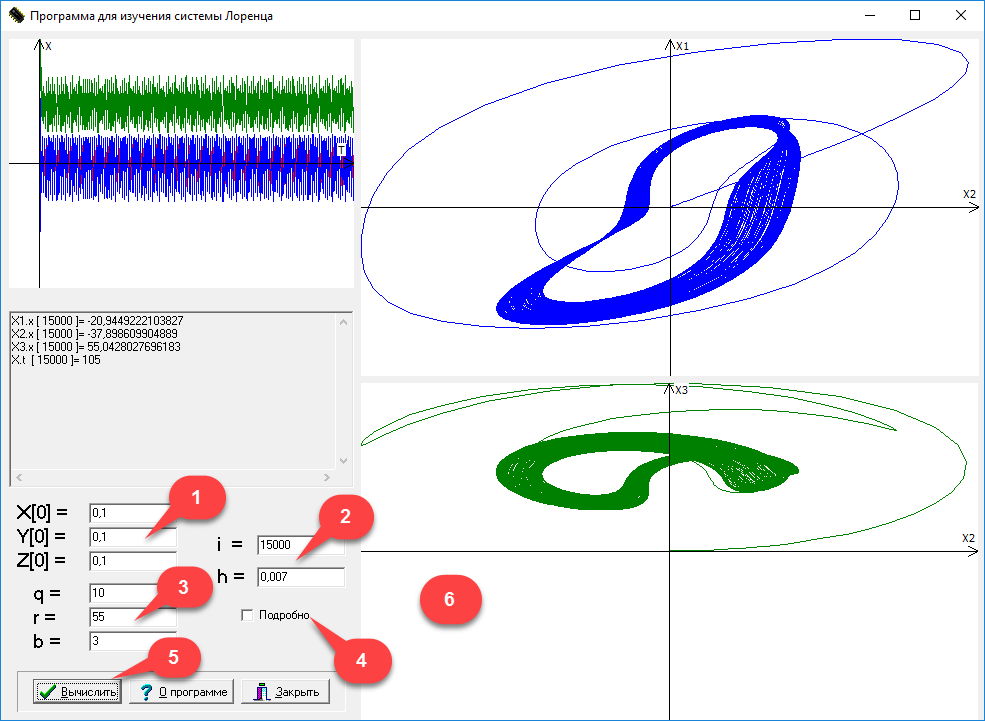
Моделирование поведения системы Лоренца с использованием программы Lorenz предполагает выполнение следующих шагов (рис.14):
- определить начальные координаты (x0,y0,z0);
- задать шаг интегрирования h и число итераций i;
- установить значение коэффициентов q, r, b;
- (опционально) установить индикатор «Подробно» для получения деталей решения;
- нажать кнопку «Вычислить»;
- (опционально) дважды щелкнуть на полученных изображениях для их копирования в буфер обмена.
Рис. 14. Последовательность шагов для запуска программы Lorenz
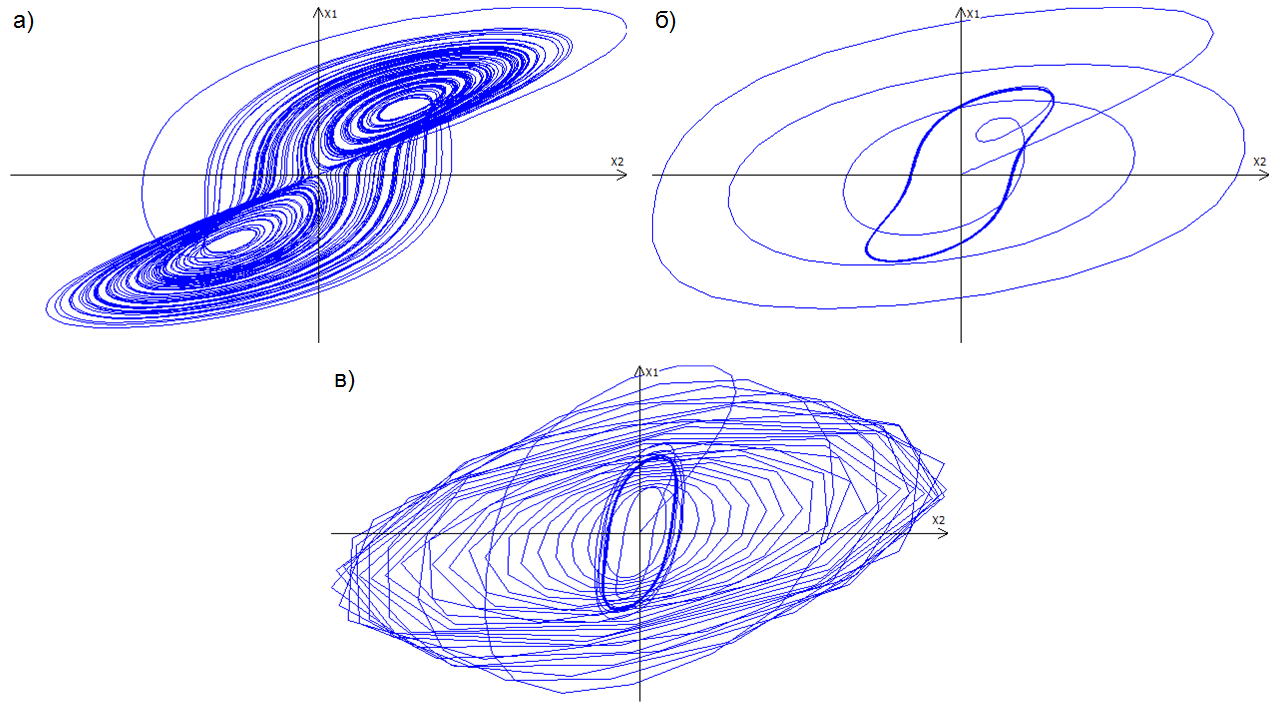
Примеры моделирования поведения системы Лоренца программой Lorenz приведены на рис.15.
Рис. 15. Примеры фазовых портретов системы Лоренца
Литература
- Архангельский А.Я. Программирование в C++ Builder. – М.: Бином-Пресс, 2010. – 1304 с.
- Кирьянов Д. Mathcad 15/Mathcad Prime 1.0. – СПб.: БХВ-Петербург, 2012. – 432 с.
- Арнольд В.И. Обыкновенные дифференциальные уравнения. – М.: МЦНМО, 2012. – 344 с.
Список программ
- MassTextReplacer - программа для массового изменения текстовых файлов;
- Lorenz - программа для изучения системы Лоренца;
- VanDerPol - программа для изучения работы генератора Ван-дер-Поля.