VanDerPol - программа для изучения работы модернизированного генератора Ван-дер-Поля

Подробности

Опубликовано: 10.07.2018 11:10

Автор: Степанов Дмитрий Юрьевич

Просмотров: 16844

Операционная система: Windows.
Лицензия: бесплатно.
Версия: 1.1.0.0.
Аннотация: демонстрируется программа по анализу генератора Ван-дер-Поля, позволяющая наблюдать такие состояния системы, как устойчивый аттрактор, устойчивый и неустойчивый фокус, предельный цикл, образование второго неустойчивого фокуса и предельного цикла.
Скачать: ZIP (архив программы).
Ключевые слова: осциллятор Ван дер Поля, уравнение Ван Дер Поля matlab, дифференциальное уравнение Ван дер Поля, уравнение Ван Дер Поля фазовый портрет, метод Ван Дер Поля пример, уравнение генератор Ван Дер Поля, метод Рунге Кутта 2 порядка, уравнение Ван дер Поля портрет, метод Ван дер Поля, осциллятор Ван дер Поля дуффинга, фазовый портрет уравнения Ван-дер-Поля, решение уравнения Ван-дер-Поля, Бальтазар Ван дер Поль, Ван дер Поль математик, Ван дер Поль маткад, Ван дер Поль уравнение, Ван дер Поль нелинейная теория электрических колебаний, Ван дер Поль программа, Ван Дер Поль генераторы, Ван дер Поль матлаб.

Осциллятор Ван-дер-Поля представляет собой генератор с нелинейным затуханием. Был предложен голландским физиком Бальтазаром Ван-дер-Полем. Ван-дер-Поль выявил колебания, позже названные предельными циклами, а также состояние детерминированного хаоса. Осциллятор Ван-дер-Поля задается дифференциальным уравнением

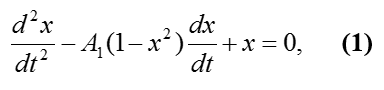
где x – координата точки, зависящая от времени t, A1 – коэффициент, характеризующий силу затухания колебаний. В результате исследования системы были выявлены нижеуказанные закономерности.

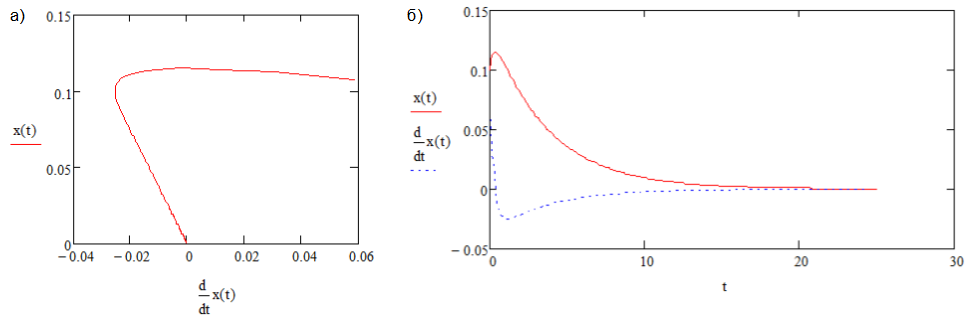
При отрицательных значениях A1<0 в системе наблюдается образование особой точки типа устойчивый узел (рис.1).

Рис. 1. Устойчивый узел, A1<0

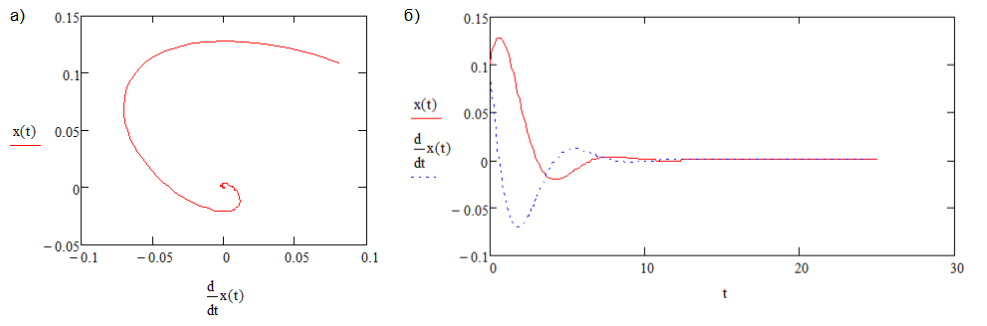
где x – координата точки, зависящая от времени t, A1 – коэффициент, характеризующий силу затухания колебаний. В результате исследования системы были выявлены нижеуказанные закономерности.

Рис. 2. Устойчивый фокус, A1<0

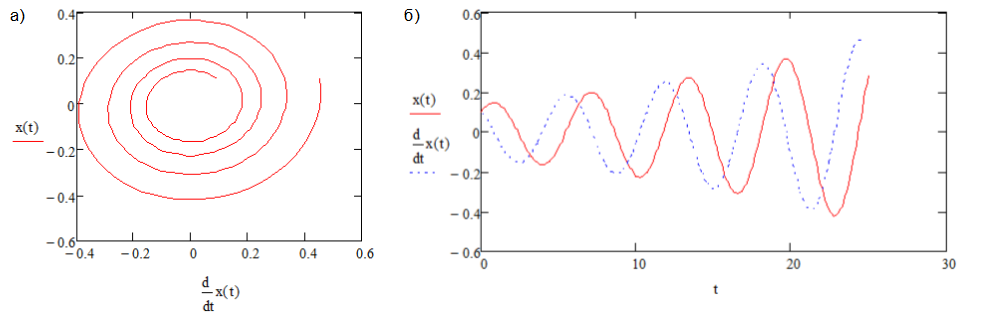
Устойчивый предельный цикл (рис.3) образуется при последующем увеличении значения A1, A1<0.

Рис. 3. Устойчивый предельный цикл, A1<0

Увеличение A1 до положительных значений (A1>0) приводит к потере устойчивости, в результате образуется особая точка вида неустойчивый фокус (рис.4).

Рис. 4. Неустойчивый фокус, A1>0

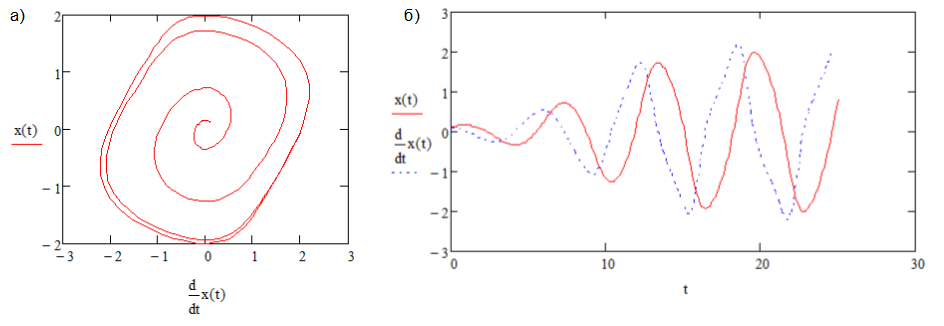
Дальнейшее увеличение A1 (A1>0) приводит к образованию неустойчивого предельного цикла (рис.5).

Рис. 5. Неустойчивый предельный цикл, A1>0

Модернизированный генератор Ван-дер-Поля позволяет наблюдать автоколебательный режим работы системы. В случае модернизированного осциллятора формула (1) преобразуется к виду (2)

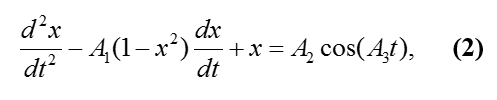
где x – координата точки, а A1, A2, A3 – коэффициенты (A2>0, 0<=A3, A3<=10).

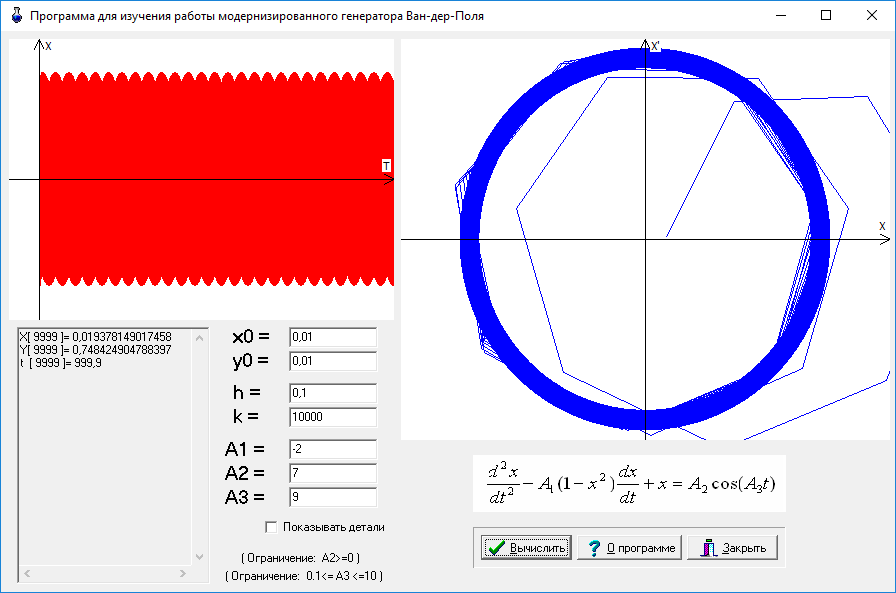
Программа «VanDerPol - программа для изучения работы модернизированного генератора Ван-дер-Поля», реализованная в среде разработки Turbo C++, позволяет смоделировать работу модернизированного генератора Ван-дер-Поля. Построение фазового портрета и графика зависимости решений от времени t ведется на основе метода Рунге-Кутта второго порядка. Интерфейс программы приведен на рис.6.

Рис. 6. Интерфейс программы для изучения работы модернизированного генератора Ван-дер-Поля

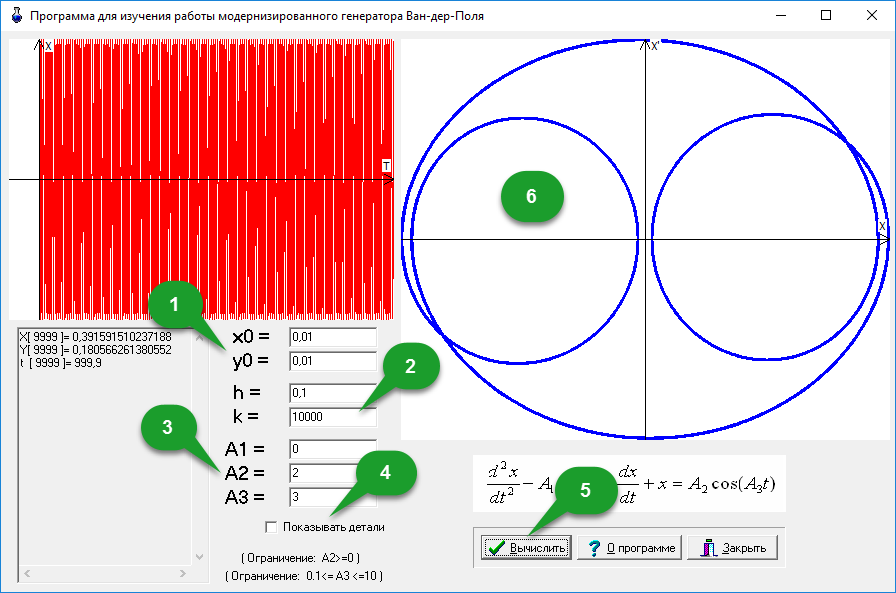
Моделирование работы модернизированного генератора с использованием программы VanDerPol предполагает выполнение следующих шагов (рис.7): 

• определить начальные координаты (x0,y0);
• задать шаг интегрирования h и число итераций k;
• установить значение коэффициентов A1, A2, A3;
• (опционально) установить индикатор «Показывать детали» для получения деталей решения;
• нажать кнопку «Вычислить»;
• (опционально) дважды щелкнуть на полученных изображениях для их копирования в буфер обмена.

Рис. 7. Последовательность шагов для запуска программы VanDerPol

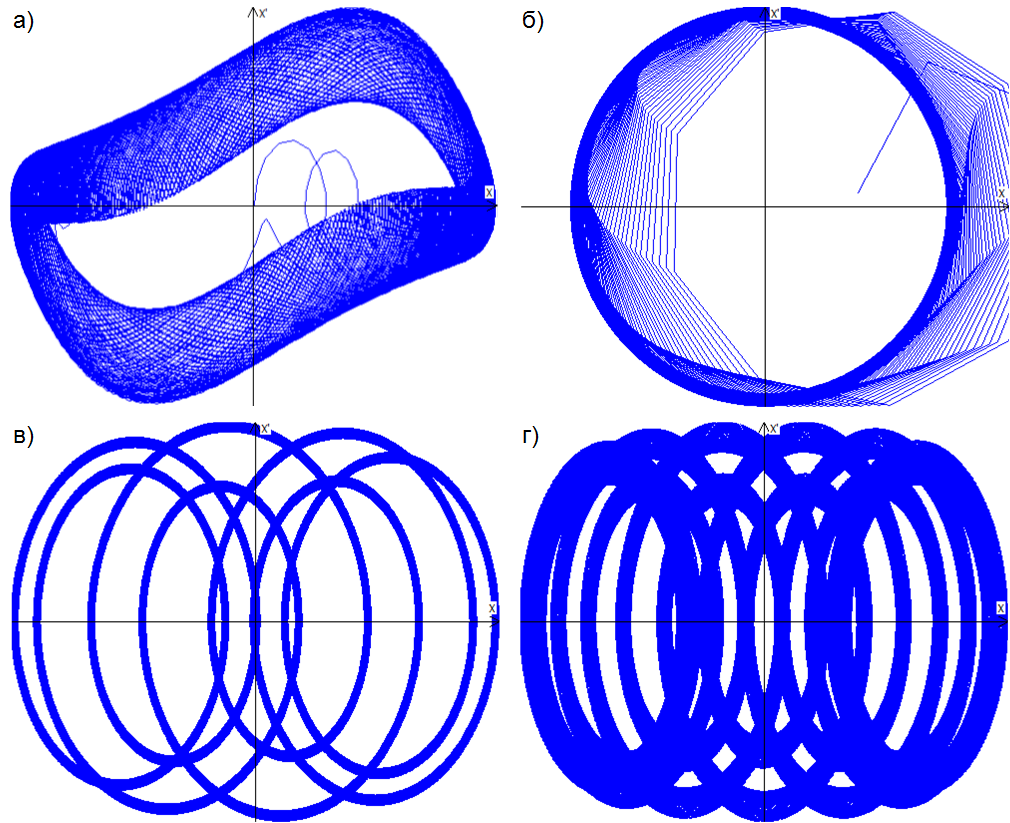
Рис. 8. Примеры фазовых портретов модернизированного генератора Ван-дер-Поля

Литература 

1. Архангельский А.Я. Программирование в C++ Builder. – М.: Бином-Пресс, 2010. – 1304 с.
2. Кирьянов Д. Mathcad 15/Mathcad Prime 1.0. – СПб.: БХВ-Петербург, 2012. – 432 с.
3. Арнольд В.И. Обыкновенные дифференциальные уравнения. – М.: МЦНМО, 2012. – 344 с. 

Список программ

1. MassTextReplacer - программа для массового изменения текстовых файлов;
2. Lorenz - программа для изучения системы Лоренца;
3. VanDerPol - программа для изучения работы генератора Ван-дер-Поля.