Дифференциальные уравнения первого порядка

Подробности

Опубликовано: 15.01.2019 10:32

Автор: Степанов Дмитрий Юрьевич

Просмотров: 4649

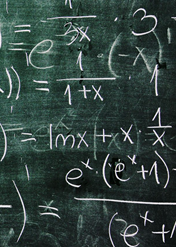
Аннотация: рассматриваются общий вид уравнения, виды уравнений, общее и частное решение, интегральная кривая, задача Коши, виды уравнений и способы их решения, численные методы решения уравнений, функции решения уравнений в MathCad, примеры решения уравнений в среде MathCad.
Скачать: PDF.
Ключевые слова: общий вид дифференциального уравнения n-го порядка, обыкновенные дифференциальные уравнения и уравнения в производных, решение дифференциального уравнения и интегральная кривая, общее и частное решение дифференциального уравнения n-го порядка, теорема Коши и ее интерпретация для дифференциального уравнения n-го порядка, виды дифференциальных уравнений 1-го порядка и способы их решения, дифференциальные уравнения 1-го порядка с разделенными переменными, дифференциальные уравнения 1-го порядка с разделяющимися переменными, дифференциальные уравнения 1-го порядка, приводящиеся к уравнениям с разделяющимися переменными, однородные дифференциальные уравнения 1-го порядка, дифференциальные уравнения 1-го порядка приводящиеся к однородным, обобщенные однородные дифференциальные уравнения 1-го порядка, линейные дифференциальные уравнения 1-го порядка решаемые методом Лагранжа, численный метод Эйлера при решении дифференциальных уравнений 1-го порядка, численный метод Рунге-Кутта при решении дифференциальных уравнений 1-го порядка, функции Odesolve и Rkfixed в MathCad для решения дифференциальных уравнений 1-го порядка, пример решения дифференциальных уравнений 1-го порядка в MathCad.